[프로그래머스] 보행자 천국 Java 풀이

이 글은 혼자 학습한 내용을 바탕으로 작성되었습니다.

틀리거나 잘못된 정보가 있을 수 있습니다.

댓글로 알려주시면 수정하도록 하겠습니다.

---

1. 문제

카카오내비 개발자인 제이지는 시내 중심가의 경로 탐색 알고리즘 개발 업무를 담당하고 있다. 최근 들어 보행자가 자유롭고 편리하게 걸을 수 있도록 보행자 중심의 교통 체계가 도입되면서 도심의 일부 구역은 자동차 통행이 금지되고, 일부 교차로에서는 보행자 안전을 위해 좌회전이나 우회전이 금지되기도 했다. 복잡해진 도로 환경으로 인해 기존의 경로 탐색 알고리즘을 보완해야 할 필요가 생겼다.

도시 중심가의 지도는 m × n 크기의 격자 모양 배열 city_map으로 주어진다. 자동차는 오른쪽 또는 아래 방향으로 한 칸씩 이동 가능하다.

city_map[i][j]에는 도로의 상황을 나타내는 값이 저장되어 있다.

• 0인 경우에는 자동차가 자유롭게 지나갈 수 있다.
• 1인 경우에는 자동차 통행이 금지되어 지나갈 수 없다.
• 2인 경우는 보행자 안전을 위해 좌회전이나 우회전이 금지된다. (왼쪽에서 오던 차는 오른쪽으로만, 위에서 오던 차는 아래쪽으로만 진행 가능하다)

도시의 도로 상태가 입력으로 주어졌을 때, 왼쪽 위의 출발점에서 오른쪽 아래 도착점까지 자동차로 이동 가능한 전체 가능한 경로 수를 출력하는 프로그램을 작성하라. 이때 가능한 경로의 수는 컴퓨터가 표현할 수 있는 정수의 범위를 넘어설 수 있으므로, 가능한 경로 수를 20170805로 나눈 나머지 값을 출력하라.

2. 입력

입력은 도시의 크기를 나타내는 m과 n, 그리고 지도를 나타내는 2차원 배열 city_map으로 주어진다. 제한조건은 아래와 같다.

• 1 <= m, n <= 500
• city_map의 크기는 m × n이다.
• 배열의 모든 원소의 값은 0, 1, 2 중 하나이다.
• 출발점의 좌표는 (0, 0), 도착점의 좌표는 (m - 1, n - 1)이다.
• 출발점과 도착점의 city_map[i][j] 값은 0이다.

3. 예제

m	n	city_map	answer
3	3	[[0, 0, 0], [0, 0, 0], [0, 0, 0]]	6
3	6	[[0, 2, 0, 0, 0, 2], [0, 0, 2, 0, 1, 0], [1, 0, 0, 2, 2, 0]]	2

4. 풀이

(1,1)에서 (m, n)까지 가는 최단 경로의 개수를 찾는 방법을 먼저 알아야 한다.

 

먼저 출발점인 (0,0)의 값을 1로 두고 시작합니다.

 

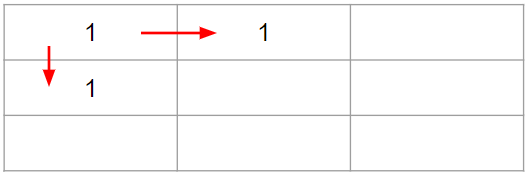
(0,0)에서 (1,0)으로 가는 방법은 1가지 이므로 (1,0)의 값은 1이 됩니다.

 

(0,0)에서 (0,1)으로 가는 방법은 1가지 이므로 (0,1)의 값은 1이 됩니다.

 

(0,0)에서 (1,1)로 가는 방법은 2가지가 존재합니다.

• 파란색 선인 (0,0) -> (0,1) -> (1,1) 순으로 이동하여 (1,1)로 가는 방법
• 초록색 선인 (0,0) -> (1,0) -> (1,1) 순으로 이동하여 (1,1)로 가는 방법

(0,0)에서 (2,1)로 가는 방법은 3가지가 존재합니다.

• 파란색 선인 (0,0) -> (0,1) -> (1,1) -> (2,1) 순으로 이동하여 (2,1)로 가는 방법
• 초록색 선인 (0,0) -> (1,0) -> (1,1) -> (2,1) 순으로 이동하여 (2,1)로 가는 방법
• 보라색 선인 (0,0) -> (1,0) -> (1,1) -> (2,1) 순으로 이동하여 (2,1)로 가는 방법

 

여기서 (0,0)에서 출발하여 (m, n)까지 가는 최단거리 개수는 DP를 이용하여 구할 수 있습니다.

 

2차원 DP 배열을 만들기 위한 점화식을 도출하여야 하는데 점화식은 DP [i][j] = DP [i-1][j] + DP [i][j-1]을 이용하여 배열을 채워 나갈 수 있습니다.

 

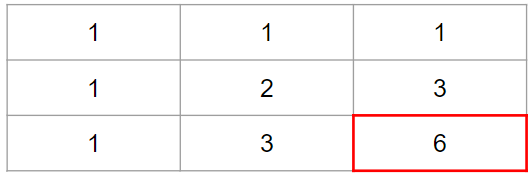
예제 1번과 같이 m=3이고 n=3이고 모든 길이 일반 도로인 경우 최단 거리 개수는 6개가 됩니다.

 

최단 거리를 구하는 방법은 구현을 하였으나 문제에서는 조건이 한 가지 더 있습니다.

 

바로 도로의 상황입니다. 

• 0인 경우에는 자동차가 자유롭게 지나갈 수 있다.
  위에서 최단거리 개수를 구할 때 도로가 모두 0인 경우를 이용하여 구하였습니다. 그러므로 0은 위와 동일하게 적용하면 됩니다.
• 1인 경우에는 자동차 통행이 금지되어 지나갈 수 없다.
  1인 경우는 지나갈 수 없는 길이기 때문에 해당 값은 점화식을 이용하지 않고 무조건 0의 값이 됩니다.

2인 경우는 보행자 안전을 위해 좌회전이나 우회전이 금지된다. (왼쪽에서 오던 차는 오른쪽으로만, 위에서 오던 차는 아래쪽으로만 진행 가능하다)
2인 경우는 좌회전과 우회전이 금지되어 직진만 가능합니다. 그러므로 점화식에 조금에 변화가 생깁니다.

지도에서 도로의 값이 2인 경우는 DP 2차원 배열에 값을 1과 동일한 0으로 두고 진행합니다.

DP 배열 (3,2)의 값을 채우기 위해 (2,2) + (3,1)의 값을 넣어야 하지만 (2,2)의 도로 값이 2이므로 해당 DP의 값은

(1,2) + (3,1)이 되어야 합니다.

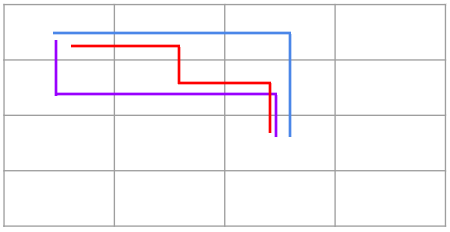
위 그림처럼 위에서 (2,2) 위치로 올 수 있는 진행 방법은 (3,2)로 진행이 불가능하기 때문입니다.

그 결과 DP(3,2)의 값은 7이 됩니다.

 

이번에는 지도의 2 값이 연속으로 있는 경우를 살펴보겠습니다.

지도에서 도로의 값이 2인 경우는 DP 2차원 배열에 값을 1과 동일한 0으로 두고 진행합니다.

DP 배열 (3,2)의 값을 채우기 위해 (2,2) + (3,1)의 값을 넣어야 하지만 (2,2)의 도로 값이 2이므로 해당 DP의 값은

(0,2) + (3,1)이 되어야 합니다.

 

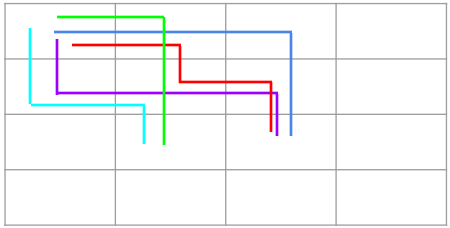
이 경우는 (1,1)에서 (1,2)로 오는 길들 과 (2,1)에서 (2,2)로 오는 길들 모두 (3,2)로 진행이 불가능합니다.

 

그 결과 DP(3,2)의 값은 5가 됩니다.

 

정리하자면 도로의 상태가 1 또는 2인 경우는 DP의 값을 0으로 입력합니다.

 

그리고 도로의 상태가 0인 경우는 현재 위치에서 왼쪽의 도로들 중 최초로 도로 값이 2가 아닌 위치를 찾고 현재 위치에서 위쪽의 도로들 중 최초로 도로 값이 2가 아닌 위치를 찾아 두 값을 더한 값이 현재 위치의 최단거리 개수가 됩니다.

 

최종 점화식을 만들면

DP[i][j] = DP[i][위쪽 최초 2가 아닌 위치] + DP[왼쪽 최초 2가 아닌 위치][j]가 됩니다.

 

5. 코드

전체 코드는 Git에 있습니다.

private int[][] cityMap;
private int[][] map;

public int solution(int m, int n, int[][] cityMap) {
	int MOD = 20170805;
	this.cityMap = cityMap;
	map = new int[m + 1][n + 1];

	for (int i = 1; i <= m; i++) {
		for (int j = 1; j <= n; j++) {
			if (i == 1 && j == 1)
				map[i][j] = 1;
			else {
				if (cityMap[i - 1][j - 1] == 0)
					map[i][j] = (getTopValue(i, j) + getLeftValue(i, j)) % MOD;
				else
					map[i][j] = 0;
			}
		}
	}

	return map[m][n];
}

public int getTopValue(int rowIndex, int columnIndex) {
	for (int i = rowIndex - 1; i > 0; i--) {
		if (cityMap[i - 1][columnIndex - 1] != 2)
			return map[i][columnIndex];
	}

	return 0;
}

public int getLeftValue(int rowIndex, int columnIndex) {
	for (int i = columnIndex - 1; i > 0; i--) {
		if (cityMap[rowIndex - 1][i - 1] != 2)
			return map[rowIndex][i];
	}

	return 0;
}