[알고리즘] Dijkstra 알고리즘

이 글은 혼자 학습한 내용을 바탕으로 작성되었습니다.

틀리거나 잘못된 정보가 있을 수 있습니다.

댓글로 알려주시면 수정하도록 하겠습니다.

---

1. Dijkstra 알고리즘이란?

음의 가중치(비용)이 없는 그래프에서 특정 한 노드에서 다른 모든 노드까지의 최단거리를 구하는 알고리즘을 말합니다.

 

다익스트라 알고리즘은 그리디와 다이나믹 프로그래밍 방법을 사용하여 구현합니다.

 

1. 다익스트라는 시작 노드에서 아직 방문하지 않은 노드들 중 최단거리 노드를 선택 합니다. (그리디 기법)
2. 다익스트라는 시작 노드에서 갈 수 있는 노드들을 방문하면서 비용이 최소면 갱신합니다. (다이나믹 프로그래밍 기법)

 

위 2가지 방법을 반복하여 특정 노드에서 나머지 모든 노드로 가는 최단거리를 구하는 알고리즘 입니다.

 

2. 알고리즘 방법

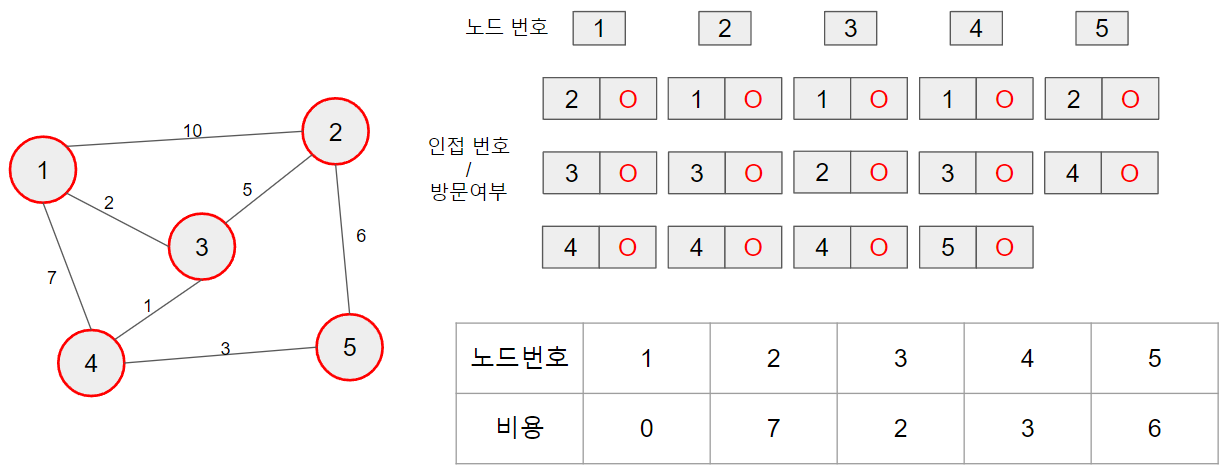
그래프에서 특정노드(시작노드)가 1번이라고 가정하고 진행하겠습니다.

Graph는 인접 List 형태로 만들고 최종 비용을 가지는 배열을 생성 후 시작 노드에서 시작노드로 가는 비용은 없으므로 0을 만들고 나머지는 모두 큰 값을 넣어 초기화 합니다.

 

 

비용 배열에서 최저 비용을 가지고 있고 방문을 하지 않은 노드인 1번 노드의 방문여부를 방문으로 변경하고 인접 노드를 확인합니다.

인접 노드는 2, 3, 4번 노드 이고 각 노드의 비용 배열의 값이 (1번 노드 비용 배열의 값 + 1번 노드 부터의 비용) 보다 작으면 비용 배열의 값을 갱신 합니다.

• 2번 노드 : 1번 노드 비용 배열의 값(0) + 1번 노드로 부터 2번 노드까지의 비용(10) = 10
  2번 노드의 경우 기존의 값이 Max이고 변경하고자 하는 값은 10이므로 10으로 변경 합니다.
  
  
• 3번 노드 : 1번 노드 비용 배열의 값(0) + 1번 노드로 부터 3번 노드까지의 비용(2) = 2
  3번 노드의 경우 기존의 값이 Max이고 변경하고자 하는 값은 2이므로 2로 변경 합니다.
  
  
• 4번 노드 : 1번 노드 비용 배열의 값(0) + 1번 노드로 부터 4번 노드까지의 비용(7) = 7
  4번 노드의 경우 기존의 값이 Max이고 변경하고자 하는 값은 7이므로 7로 변경 합니다.

 

다음 비용 배열에서 최저 비용을 가지고 있고 방문을 하지 않은 노드인 3번 노드의 방문여부를 방문으로 변경하고 인접 노드를 확인합니다.

인접 노드는 1, 2, 4번 노드 이고 각 노드의 비용 배열의 값이 (3번 노드 비용 배열의 값 + 3번 노드 부터의 비용) 보다 작으면 비용 배열의 값을 갱신 합니다.

• 1번 노드 : 3번 노드 비용 배열의 값(2) + 3번 노드로 부터 1번 노드까지의 비용(2) = 4
  1번 노드의 경우 기존의 값이 0이고 변경하고자 하는 값은 4이므로 변경을 하지 않습니다.
  
  
• 2번 노드 : 3번 노드 비용 배열의 값(2) + 3번 노드로 부터 2번 노드까지의 비용(5) = 7
  2번 노드의 경우 기존의 값이 10이고 변경하고자 하는 값은 7이므로 7로 변경 합니다.
  
  
• 4번 노드 : 3번 노드 비용 배열의 값(2) + 3번 노드로 부터 4번 노드까지의 비용(1) = 3
  4번 노드의 경우 기존의 값이 7이고 변경하고자 하는 값은 3이므로 3으로 변경 합니다.

 

다음 비용 배열에서 최저 비용을 가지고 있고 방문을 하지 않은 노드인 4번 노드의 방문여부를 방문으로 변경하고 인접 노드를 확인합니다.

인접 노드는 1, 3, 5번 노드 이고 각 노드의 비용 배열의 값이 (4번 노드 비용 배열의 값 + 4번 노드 부터의 비용) 보다 작으면 비용 배열의 값을 갱신 합니다.

• 1번 노드 : 4번 노드 비용 배열의 값(3) + 4번 노드로 부터 1번 노드까지의 비용(7) = 10
  1번 노드의 경우 기존의 값이 0이고 변경하고자 하는 값은 10이므로 변경을 하지 않습니다.
  
  
• 3번 노드 : 4번 노드 비용 배열의 값(3) + 4번 노드로 부터 3번 노드까지의 비용(1) = 4
  3번 노드의 경우 기존의 값이 2이고 변경하고자 하는 값은 4이므로 변경을 하지 않습니다.
  
  
• 5번 노드 : 4번 노드 비용 배열의 값(3) + 4번 노드로 부터 5번 노드까지의 비용(3) = 6
  5번 노드의 경우 기존의 값이 Max이고 변경하고자 하는 값은 6이므로 6으로 변경 합니다.

 

다음 비용 배열에서 최저 비용을 가지고 있고 방문을 하지 않은 노드인 5번 노드의 방문여부를 방문으로 변경하고 인접 노드를 확인합니다.

인접 노드는 2, 4번 노드 이고 각 노드의 비용 배열의 값이 (5번 노드 비용 배열의 값 + 5번 노드 부터의 비용) 보다 작으면 비용 배열의 값을 갱신 합니다.

• 2번 노드 : 5번 노드 비용 배열의 값(6) + 5번 노드로 부터 2번 노드까지의 비용(6) = 12
  1번 노드의 경우 기존의 값이 0이고 변경하고자 하는 값은 12이므로 변경을 하지 않습니다.
  
  
• 4번 노드 : 5번 노드 비용 배열의 값(6) + 5번 노드로 부터 4번 노드까지의 비용(3) = 9
  3번 노드의 경우 기존의 값이 2이고 변경하고자 하는 값은 9이므로 변경을 하지 않습니다.

 

다음 비용 배열에서 최저 비용을 가지고 있고 방문을 하지 않은 노드인 2번 노드의 방문여부를 방문으로 변경하고 인접 노드를 확인합니다.

인접 노드는 1, 3, 5번 노드 이고 각 노드의 비용 배열의 값이 (4번 노드 비용 배열의 값 + 4번 노드 부터의 비용) 보다 작으면 비용 배열의 값을 갱신 합니다.

• 1번 노드 : 2번 노드 비용 배열의 값(7) + 2번 노드로 부터 1번 노드까지의 비용(10) = 17
  1번 노드의 경우 기존의 값이 0이고 변경하고자 하는 값은 17이므로 변경을 하지 않습니다.
  
  
• 3번 노드 : 2번 노드 비용 배열의 값(7) + 2번 노드로 부터 3번 노드까지의 비용(5) = 12
  3번 노드의 경우 기존의 값이 2이고 변경하고자 하는 값은 12이므로 변경을 하지 않습니다.
  
  
• 5번 노드 : 2번 노드 비용 배열의 값(7) + 2번 노드로 부터 5번 노드까지의 비용(6) = 13
  5번 노드의 경우 기존의 값이 6이고 변경하고자 하는 값은 13이므로 변경을 하지 않습니다.

 

최종적으로 시작노드인 1번 노드에서 출발하여 각 노드로 가는 최소비용은

• 2번 노드 = 7
• 3번 노드 = 2
• 4번 노드 = 3
• 5번 노드 = 6

이 됩니다.

 

3. 구현 코드

전체 코드는 Git에 있습니다.

 

• For문을 이용한 구현 코드

public static void loopDijkstra(int startNum, int nodeCnt, int[][] graphArr) {
	List<List<DestNode>> graph = new ArrayList<>();
	for (int i = 0; i < nodeCnt + 1; i++)
		graph.add(new ArrayList<>());

	for (int[] ints : graphArr) {
		graph.get(ints[0]).add(new DestNode(ints[1], ints[2]));
		graph.get(ints[1]).add(new DestNode(ints[0], ints[2]));
	}

	boolean[] check = new boolean[nodeCnt + 1];

	int[] costs = new int[nodeCnt + 1];
	Arrays.fill(costs, Integer.MAX_VALUE);

	costs[startNum] = 0;

	for (int i = 0; i < nodeCnt; i++) {
		int minCost = Integer.MAX_VALUE;
		int minNodeNum = 0;

		for (int j = 1; j < costs.length; j++) {
			if (!check[j] && minCost > costs[j]) {
				minCost = costs[j];
				minNodeNum = j;
			}
		}

		check[minNodeNum] = true;

		for (int j = 0; j < graph.get(minNodeNum).size(); j++) {
			DestNode node = graph.get(minNodeNum).get(j);

			if (costs[node.destNum] > node.cost + costs[minNodeNum])
				costs[node.destNum] = node.cost + costs[minNodeNum];
		}
	}

	System.out.println(Arrays.toString(costs));
}

public static class DestNode {
	private final int destNum;
	private final int cost;

	public DestNode(int destNum, int cost) {
		this.destNum = destNum;
		this.cost = cost;
	}
}

 

• Queue를 이용한 구현 코드

public static void queueDijkstra(int startNum, int nodeCnt, int[][] graphArr) {
	List<List<DestNode>> graph = new ArrayList<>();
	for (int i = 0; i < nodeCnt + 1; i++)
		graph.add(new ArrayList<>());

	for (int[] ints : graphArr) {
		graph.get(ints[0]).add(new DestNode(ints[1], ints[2]));
		graph.get(ints[1]).add(new DestNode(ints[0], ints[2]));
	}

	int[] costs = new int[nodeCnt + 1];
	Arrays.fill(costs, Integer.MAX_VALUE);

	costs[startNum] = 0;

	Queue<DestNode> queue = new LinkedList<>();
	queue.offer(new DestNode(startNum, 0));

	while (!queue.isEmpty()) {
		DestNode node = queue.poll();

		for (int i = 0; i < graph.get(node.destNum).size(); i++) {
			DestNode compareNode = graph.get(node.destNum).get(i);

			if (costs[compareNode.destNum] > node.cost + compareNode.cost) {
				queue.offer(new DestNode(compareNode.destNum, node.cost + compareNode.cost));
				costs[compareNode.destNum] = node.cost + compareNode.cost;
			}
		}
	}

	System.out.println(Arrays.toString(costs));
}

public static class DestNode {
	private final int destNum;
	private final int cost;

	public DestNode(int destNum, int cost) {
		this.destNum = destNum;
		this.cost = cost;
	}
}