[알고리즘] Floyd Warshall

이 글은 혼자 학습한 내용을 바탕으로 작성되었습니다.

틀리거나 잘못된 정보가 있을 수 있습니다.

댓글로 알려주시면 수정하도록 하겠습니다.

---

1. floyd warshall 알고리즘이란?

음의 사이클이 없는 그래프에서 모든 정점에서 다른 모든 정점으로의 최단 거리를 구하는 알고리즘 이며 음의 간선이 존재하여도 최단 거리를 구할 수 있습니다. 또한 floyd warshall 알고리즘은 경유하는 정점을 기준으로 최단거리를 구해나가는 알고리즘 입니다.

 

2. Dijkstra VS floyd warshall

floyd warshall알고리즘과 Dijkstra 알고리즘은 유사 하지만 조금씩의 차이점이 있습니다.

• Dijkstra는 특정 정점에서의 최단 거리를 구하는 알고리즘이고 floyd warshall은 모든 정점의 최단거리를 구하는 알고리즘 입니다. Dijkstra를 모든 정점의 최단거리를 구한 결과와 floyd warshall 결과가 같습니다.
• Dijkstra는 음의 간선이 존재하면 알고리즘 적용이 불가능 하지만 floyd warshall은 음의 간선이 존재하여도 음의 사이클이 발생하지 않으면 적용이 가능 합니다.
  
  

3. 알고리즘 방법

floyd warshall은 경유하는 정점을 기준으로 최단 거리를 구하는 알고리즘 이므로 경유 정점은 1부터 최대 노드까지 이고 출발지, 도착지 또한 1부터 최대 노드까지 입니다.

 

최소 비용을 구하는 방법은 기존 비용 2차원 배열의 값 보다 경유지를 거치고 도착한 비용이 더 작은 경우 비용 2차원 배열의 값을 갱신합니다.

 

즉 Min(기존 2차원 배열의 값, 출발지 ->  경유지의 비용 + 경유지 -> 도착지의 비용)이 됩니다.

 

※비용 2차원 배열의 [i][j]는 i에서 출발하여 j에 도착하는 것을 의미합니다.

 

노드의 수 만큼 2차원 배열을 만들고 해당 배열에 간선의 비용들을 모두 입력하여 줍니다.

출발 노드와 도착 노드가 같은 경우는 비용을 0으로 입력하고 만약 노드와 노드 사이가 간선으로 이어지지 않았다면 큰 수를 넣어 표시하여 줍니다.

 

floyd warshall은 경유하는 정점을 기준으로 최단 거리를 구하는 알고리즘 이므로 첫 경유 정점은 1이 되고 출발지는 1부터 5까지 도착지 또한 1부터 5까지의 노드가 됩니다.

 

경유지 = 1 출발지 = 1 도착지 = 1인 경우

• 기존 비용 2차원 배열에 있는 값 (배열[1][1]) = 0
• 경유지 1을 거치고 도착한 값(배열[1][1] + 배열[1][1]) = 0 + 0 = 0

기존의 값은 0이고 경유지를 거치고 도착한 값이 0이므로 값을 변경하지 않습니다.

 

경유지 = 1 출발지 = 1 도착지 = 2인 경우

• 기존 비용 2차원 배열에 있는 값 (배열[1][2]) = 10
• 경유지 1을 거치고 도착한 값(배열[1][1] + 배열[1][2]) = 0 + 10 = 10

기존의 값은 10이고 경유지를 거치고 도착한 값이 10이므로 값을 변경하지 않습니다.

 

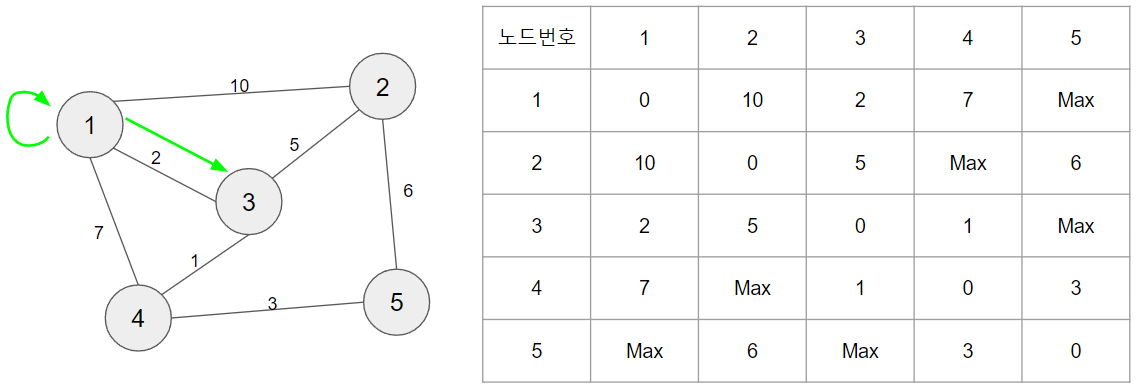
경유지 = 1 출발지 = 1 도착지 = 3인 경우

• 기존 비용 2차원 배열에 있는 값 (배열[1][3]) = 2
• 경유지 1을 거치고 도착한 값(배열[1][1] + 배열[1][3]) = 0 + 2 = 2

기존의 값은 2이고 경유지를 거치고 도착한 값이 2이므로 값을 변경하지 않습니다.

---

경유지 = 1 출발지 = 2 도착지 = 4인 경우

• 기존 비용 2차원 배열에 있는 값 (배열[2][4]) = Max
• 경유지 1을 거치고 도착한 값(배열[2][1] + 배열[1][4]) = 10 + 7 = 17

기존의 값은 Max이고 경유지를 거치고 도착한 값이 17이므로 값을 17로 변경합니다.

---

경유지 = 1 출발지 = 4 도착지 = 2인 경우

• 기존 비용 2차원 배열에 있는 값 (배열[4][2]) = Max
• 경유지 1을 거치고 도착한 값(배열[4][1] + 배열[1][2]) = 7 + 10 = 17

기존의 값은 Max이고 경유지를 거치고 도착한 값이 17이므로 값을 17로 변경합니다.

---

이렇게 모든 노드에 대한 경유지와 출발지 도착지를 구하여 진행을 하면 최종적으로 비용 2차원 배열은 위 표처럼 완성이 됩니다.

 

4. 구현 코드

전체 코드는 Git에 있습니다.

int maxValue = 1000000000;
int[][] graph = new int[nodeCnt][nodeCnt];

for (int i = 0; i < nodeCnt; i++) {
	Arrays.fill(graph[i], maxValue);
	graph[i][i] = 0;
}

for (int[] ints : graphArr) {
	graph[ints[0] - 1][ints[1] - 1] = ints[2];
	graph[ints[1] - 1][ints[0] - 1] = ints[2];
}

for (int i = 0; i < nodeCnt; i++) {
	for (int j = 0; j < nodeCnt; j++) {
		for (int k = 0; k < nodeCnt; k++)
			graph[j][k] = Math.min(graph[j][k], graph[j][i] + graph[i][k]);
	}
}

for (int i = 0; i < nodeCnt; i++) {
	for (int j = 0; j < nodeCnt; j++) {
		if (graph[i][j] == maxValue)
			System.out.print("MAX ");
		else
			System.out.print(graph[i][j] + " ");
	}
	System.out.println();
}