[프로그래머스] 스티커모으기(2) Java풀이

이 글은 혼자 학습한 내용을 바탕으로 작성되었습니다.

틀리거나 잘못된 정보가 있을 수 있습니다.

댓글로 알려주시면 수정하도록 하겠습니다.

---

1. 문제

N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.

원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.

예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.

2. 입력

• sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
• sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
• 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

3. 예제

sticker	answer
[14, 6, 5, 11, 3, 9, 2, 10]	36
[1, 3, 2, 5, 4]	8

4. 풀이

위 그림 처럼 원형인 스티커를 잘라 한줄인 스티커로 만들 수 있다.

 

이제 문제를 원형 스티커가 아닌 한줄의 스티커로 진행해 보겠습니다.

 

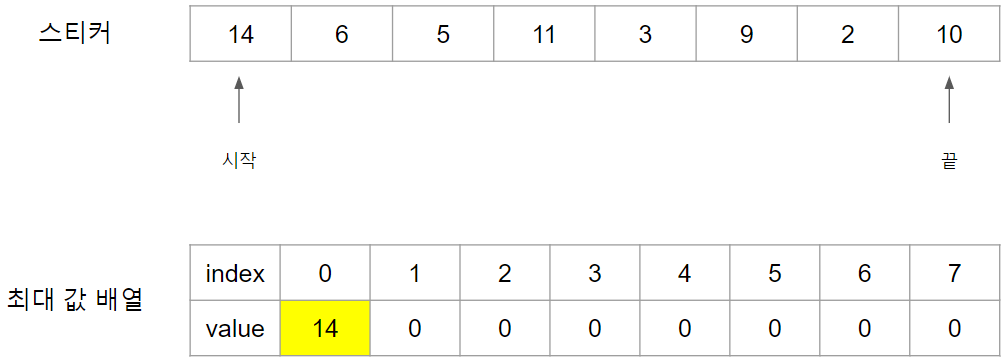
첫 스티커인 14번 스티커를 때면 최대 값 배열에 14를 Index 0번에 넣습니다.

 

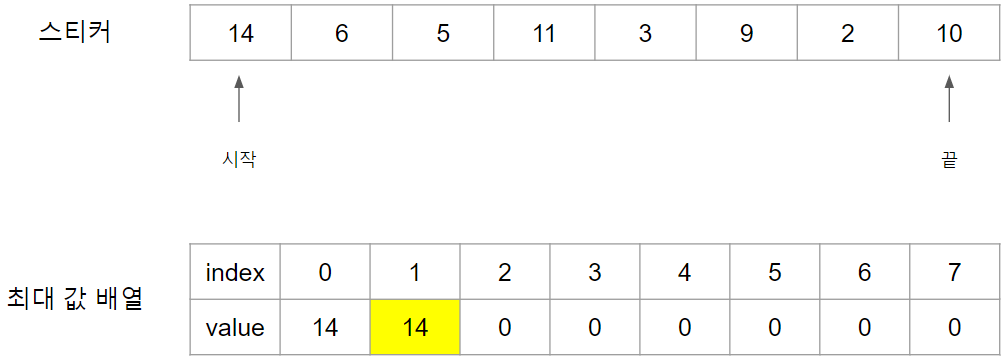
2번째 스티커인 6의 경우 14번의 스티커를 사용하였으므로 6번은 사용할 수 없습니다. 하여 이전 스티커 값인 14를 Index 1번에 넣습니다.

 

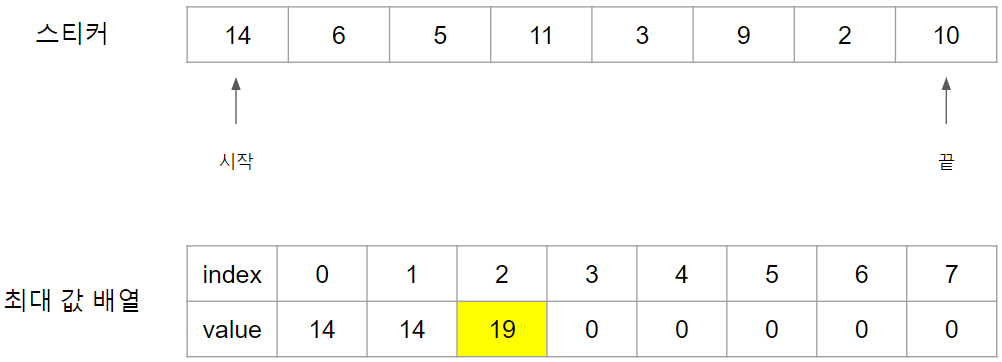
3번째 스티커인 5의 경우는 2가지 경우가 있을 수 있습니다.

• 5 스티커 이전인 6번까지 스티커를 사용을 하고 5번은 사용하지 않는 경우
  이 경우는 6번까지 선정한 스티커를 사용하고 5번 스티커를 사용하지 않을 때 이므로 14가 됩니다.
• 5 스티커의 2번째 전인 14번까지 스티커를 사용하고 5번을 사용하는 경우
  이 경우는 14번까지 선정한 스티커를 사용하고 5번 스티커를 사용하는 경우로 14 + 5의 값인 19가 됩니다.
  
  
• 위 두 경우 중 큰 값인 19가 Index 2번의 값이 됩니다.

 

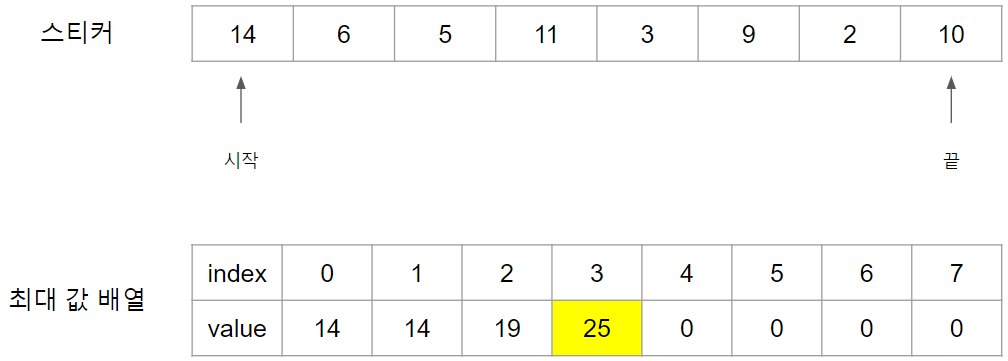
4번째 스티커인 11의 경우는 2가지 경우가 있을 수 있습니다.

• 11 스티커 이전인 5번까지 스티커를 사용을 하고 11번은 사용하지 않는 경우
  이 경우는 5번까지 선정한 스티커를 사용하고 11번 스티커를 사용하지 않을 때 이므로 19가 됩니다.
  
  
• 11 스티커의 2번째 전인 6번까지 스티커를 사용하고 11번을 사용하는 경우
  이 경우는 6번까지 선정한 스티커를 사용하고 11번 스티커를 사용하는 경우로 14 + 11의 값인 25가 됩니다.
  
  
• 위 두 경우 중 큰 값인 25가 Index 3번의 값이 됩니다.

 

위 과정을 통해 최대 값 배열을 채워 넣을 수 있는 공식을 확인 할 수 있습니다. 즉 점화식을 구할 수 있습니다.

 

점화식은 Array[i] = Max( Array[i-1] , Array[i-2] + Sticker[i] )가 됩니다.

 

---

 

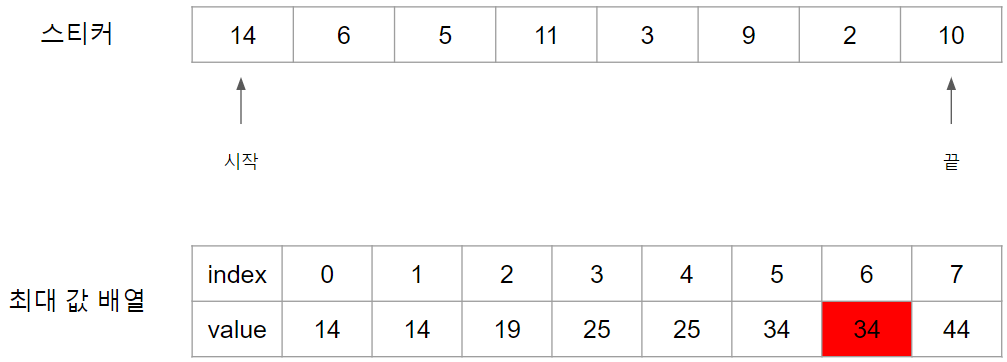
위 과정을 반복하여 최대 값 배열을 완성 시키면 위 그림과 같은 값이 완성됩니다. 여기서 주의 해야하는 것은 첫 스티커를 사용하였기 때문에 맨 마지막 값은 사용할 수 없는 값이므로 첫번째 스티커를 사용하면 최대 값은 34가 됩니다.

 

여기서 문제 풀이가 종료되면 좋겠지만 아직 하나의 과정이 더 남았습니다.

 

원형의 스티커 이므로 두 번째 스티커를 시작으로 최대 값 배열을 만들었을 때 최대 값을 구해야 합니다.

 

이번에는 위 과정과 동일하지만 2번째 스티커 부터 시작해 보겠습니다.

2번째 스티커인 6번 스티커를 때면 최대 값 배열에 6를 Index 1번에 넣습니다. 첫번째의 경우 사용할 수 없으므로 0으로 넣습니다.

 

3번째 스티커인 5의 경우 6번의 스티커를 사용하였으므로 5번은 사용할 수 없습니다. 하여 이전 스티커 값인 6을 Index 2번에 넣습니다.

 

4번째 스티커인 11의 경우는 2가지 경우가 있을 수 있습니다.

• 11 스티커 이전인 5번까지 스티커를 사용을 하고 11번은 사용하지 않는 경우
  이 경우는 5번까지 선정한 스티커를 사용하고 11번 스티커를 사용하지 않을 때 이므로 6이 됩니다.
  
  
• 11 스티커의 2번째 전인 6번까지 스티커를 사용하고 11번을 사용하는 경우
  이 경우는 6번까지 선정한 스티커를 사용하고 11번 스티커를 사용하는 경우로 6 + 11의 값인 17이 됩니다.
  
  
• 위 두 경우 중 큰 값인 17이 Index 3번의 값이 됩니다.

 

5번째 스티커인 3의 경우는 2가지 경우가 있을 수 있습니다.

• 3 스티커 이전인 11번까지 스티커를 사용을 하고 3번은 사용하지 않는 경우
  이 경우는 11번까지 선정한 스티커를 사용하고 11번 스티커를 사용하지 않을 때 이므로 17이 됩니다.
  
  
• 3 스티커의 2번째 전인 5번까지 스티커를 사용하고 3번을 사용하는 경우
  이 경우는 5번까지 선정한 스티커를 사용하고 3번 스티커를 사용하는 경우로 6 + 3의 값인 9가 됩니다.
  
  
• 위 두 경우 중 큰 값인 17이 Index 4번의 값이 됩니다.

 

---

 

위 과정을 반복하여 최대 값 배열을 완성 시키면 위 그림과 같은 값이 완성됩니다. 여기서 주의 해야하는 것은 두 번째 스티커를 사용했기 때문에 맨 마지막 값이 사용 가능해 최대값은 36이 됩니다.

 

이제 첫번째 스티커를 시작으로 만든 최대값 34와 2번째 스티커를 시작으로 만든 최대값인 36 중 큰 값인 36이 해당 원형 스티커의 최대 값인 됩니다.

 

풀이 과정을 정리하면

• 점화식인 Array[i] = Max( Array[i-1] , Array[i-2] + Sticker[i] )
• 점화식을 첫번째 스티커에서 부터 적용하여 DP 배열을 만든 뒤 Max 값인 Length - 2 값을 찾는다.
• 점화식을 2번째 스티커에서 부터 적용하여 DP 배열을 만든 뒤 Max 값인 Length - 1 값을 찾는다.
• 위 두 과정을 통해 찾은 Max값 중 큰 값이 해당 원형 스티커의 최대 값이 된다.

 

5. 코드

전체 코드는 Git에 있습니다.

if(sticker.length == 1)
	return sticker[0];

int[] dp = new int[sticker.length + 2];

for (int i = 3; i < dp.length; i++)
	dp[i] = Math.max(dp[i - 1], dp[i - 2] + sticker[i - 2]);
    
int secondMax = dp[dp.length - 1];

for (int i = 2; i < dp.length; i++)
	dp[i] = Math.max(dp[i - 1], dp[i - 2] + sticker[i - 2]);
    
int firstMax = dp[dp.length - 2];

return Math.max(firstMax, secondMax);